Tipi-3-1
Discovered by
Info
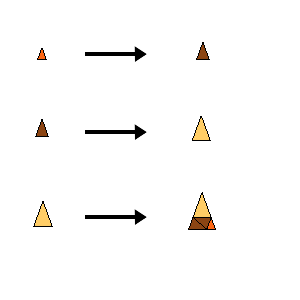
One example in a series of substitutions with inflation factor $\sqrt{s}$, where $s^m-s^k-1=0$.
The parameters m and k are arbitrary integers with m>k, m>2, k>0.
It seems that all these tilings show statistical circular symmetry. Click on ‘Infinite rotations’ above in order to see more examples of statistical circular symmetric tilings.
The substitution is a slight variation of the substitution underlying Chaim’s cubic PV.
The trick is that the free parameter in Chaim’s rule is choosen such that the prototiles become equilateral triangles. This allows to flip (reflect) tiles in the substitution, which in turn causes the infinitely many orientations, i.e., statistical circular symmetry.
Substitution Rule
Patch
