Trihex
Discovered by
Info
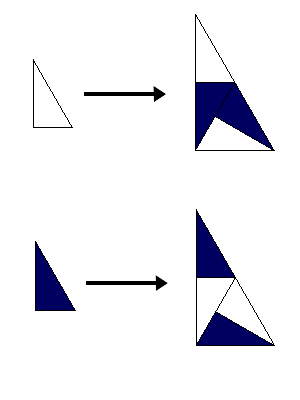
A simple rule to generate nonperiodic tilings with one prototile, a triangle with angles 30°, 60°, 90°. It looks pretty much periodic: the hexagonal patches cover 75% of the plane, and this part is clearly periodic. The triangles in between the hexagons destroy the periodicity. But, by the selfsimilarity of the tilings, one finds larger periodic subsets in the tiling, covering 93,75%, 98,44%… of the plane. Thus, the tiling is limitperiodic.
Moreover, in each patch, there is at most one tile which is not contained in a periodic subset of the tiling. The latter is not true in general for limitperiodic tilings. For instance, in the chair tiling, there can be infinitely many tiles which are not contained in any periodic subset of the chair tiling. In the language of model sets: In the trihex tilings, there is at most one tile corresponding arising from the boundary of the window.
Substitution Rule
Patch
