Cesi's Substitution
Discovered by
Info
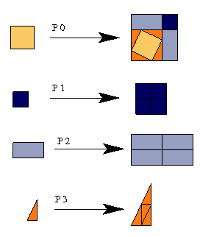
The substitution system uses 4 letters. With:
$x = \frac{\pi}{7}$, $c = \cos(x)$ and $s = \sin(x)$
They are: two squares of side lengths $1$ and $2-c-s$; a rectangle with sides $c+s$ and $2-c-s$: and a right triangle with legs $c$ and $s$.
The substitution is indicated in the figure. Up to our knowledge, this was the first example of a substitution where the tiles occur in infinitely many orientations.
Obviously, the substitution is not primitive.
Important: The substitution must be started with the large square to get anything interesting.
Substitution Rule
Patch
