Fibonacci

• Canonical Substitution Tiling
• Finite Rotations
• MLD Class Fibonacci
• One Dimensional
• Parallelogram Tiles
• Polytopal Windowed Tiling
• Self-Similar Substitution

Info

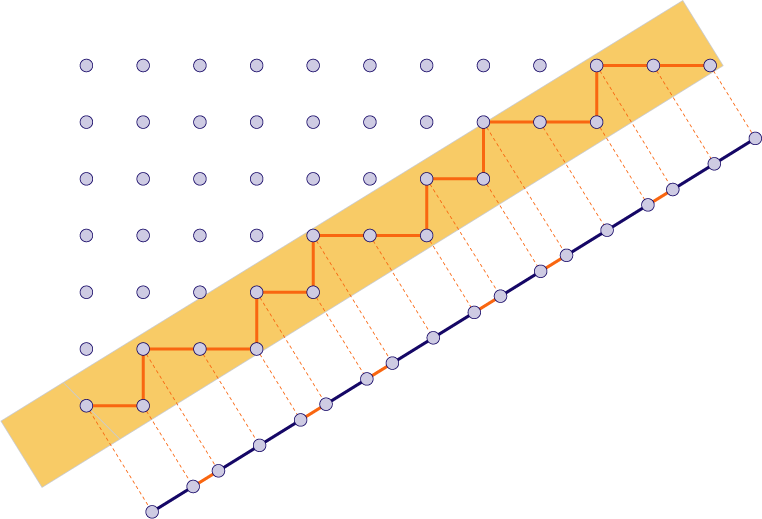
The classical example to explain the cut and project method (see figure, lower part): In the standard square lattice $\mathbb{Z}^2$, choose a stripe with slope $\frac{1}{\tau}$ (where tau is the golden ratio $\frac{1+\sqrt{5}}{2}$ ) of a certain width $\cos(\arctan(\frac{1}{\tau})) + \sin(\arctan(\frac{1}{\tau})) = \frac{1+\tau}{\sqrt{2+\tau}}$. Then take all lattice points within the strip and project them orthogonally to a line parallel to the strip. This yields a sequence of points. There are two values of distances between neighboured points, say, $S$ (short) and $L$ (long). Interpreting the point set as a partition of the line into long and short intervals yields a tiling of the line. This is the Fibonacci Tiling. 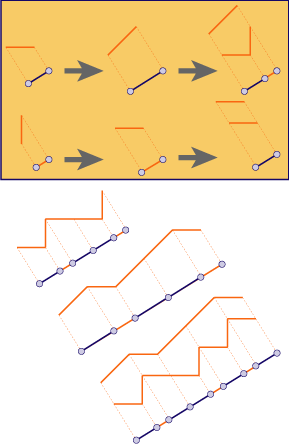It can also be generated by a substitution (see figure, upper part): A long tile $L$ becomes one short and one long tile, a short tile $S$ becomes one long tile. Thus, iterating the substitution yields the sequences $S, L, SL, LSL, SLLSL, LSLSLLSL, SLLSLLSLSLLSL, \ldots$ of length $1, 1, 2, 3, 5, 8, 13 \ldots$ respectively, which explains the name. The term ‘Fibonacci sequence’ usually refers to such symbolic sequences, made of two letters, where the term ‘Fibonacci tiling’ refers to the tiling of the line by two kinds of intervals. Each letter S corresponds to an interval of length 1, each letter $L$ corresponds to an interval of length tau (up to scaling, any two values with ratio $\frac{1}{\tau}$ will do). Fibonacci sequences occur in Penrose Rhomb tilings, at least in two ways: They describe the structure of Conway worms, and also the sequence of distances of parallel Ammann bars.

Substitution Rule

Patch

---