Golden Pinwheel
Discovered by
Info
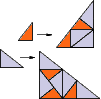
Using the prototiles of the golden triangle tiling, this substitution yields tilings where the tiles occur in infinitely many orientations. The inflation factor is $\tau + 1 = 2.618033988 \ldots $, the square of the golden mean. This is a PV number of algebraic degree 2. The expansion contains no rotational part. Nevertheless, the first substitution of the larger tile shows two small tiles, rotated against each other by an angle a incommensurate to pi (i.e., $\frac{a}{\pi}$ is irrational).
This suffices to show that the tiles occur in infinitely many orientations.
Substitution Rule
Patch
