Golden Triangle
- Finite Rotations
- Polytopal Tiles
- Polytopal Windowed Tiling
- Self-Similar Substitution
- With Decoration
Discovered by
Info
The substitution can be expressed by using the real inflation factor $\sqrt{\tau} = 1.272\ldots$, where $\tau=\frac{\sqrt{5}+1}{2}$ is the golden mean. This factor is not a PV number. Nevertheless, the tiling is pure point diffractive, and it is a cut and project tiling, see [Gel97]
, [Dv00]
. Thus the right point of view is to consider it as a tiling with the inflation factor sqrt(-tau), which is a complex PV number.
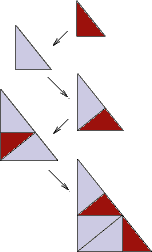
It is easy to see that there are no matching rules for the undecorated tiles. Nevertheless, in [Dv00]
a matching rule is obtained for the coloured golden triangle tilings. The golden triangle tilings are locally derivable (see mld) from the coloured ones.
This tiling is the dual tiling of the Ammann Chair, see [Gel97]
, [Fre05]
.
Substitution Rule
Patch

References
[Dv00]
Danzer, Ludwig and van Ophuysen, Gerrit
A species of planar triangular tilings with inflation factor $\sqrt{-\tau}$
Res. Bull. Panjab Univ. Sci.
2000,
50, 1-4,
pp. 137--175 (2001),
2003f:52015
[Fre05]
Frettlöh, D
Duality of model sets generated by substitutions
Rev. Roumaine Math. Pures Appl.
2005,
50,
pp. 619-639,
[Gel97]
Gelbrich, G
Fractal Penrose tiles II. Tiles with fractal boundary as duals of Penrose triangles
Aequationes Math.
1997,
54,
pp. 108--116,
MR1466298