Pinwheel

Discovered by

Info

This substitution tiling is the example of substitution tilings with infinite rotations. Its statistical and dynamical properties were studied in several papers by C. Radin, see for instance [Rad92] , [Rad97] . In particular, it was shown that the orientations of triangles in the pinwheel tiling are equally distributed in the circle. Despite the occurrance of irrational edge lengths and incommensurate angles, all vertices of the pinwheel tiling have rational coordinates. In [Rad94] , Radin established a local matching rule (with decoration) for the pinwheel tiling. Besides this one (and the kite-domino version) and the generalized pinwheel tilings of L. Sadun there are very few substitution tilings known which show infinite rotations. The colours in the images on this page are based on the orientations of the tiles.

An idea of the orientations of the tiles is given in the picture below. In this picture tiles have the same colour when reflected in the horizontal axis or rotated through $\frac{\pi}{2}$.

Pinwheel Angles

Substitution Rule

Rule Pinwheel

Patch

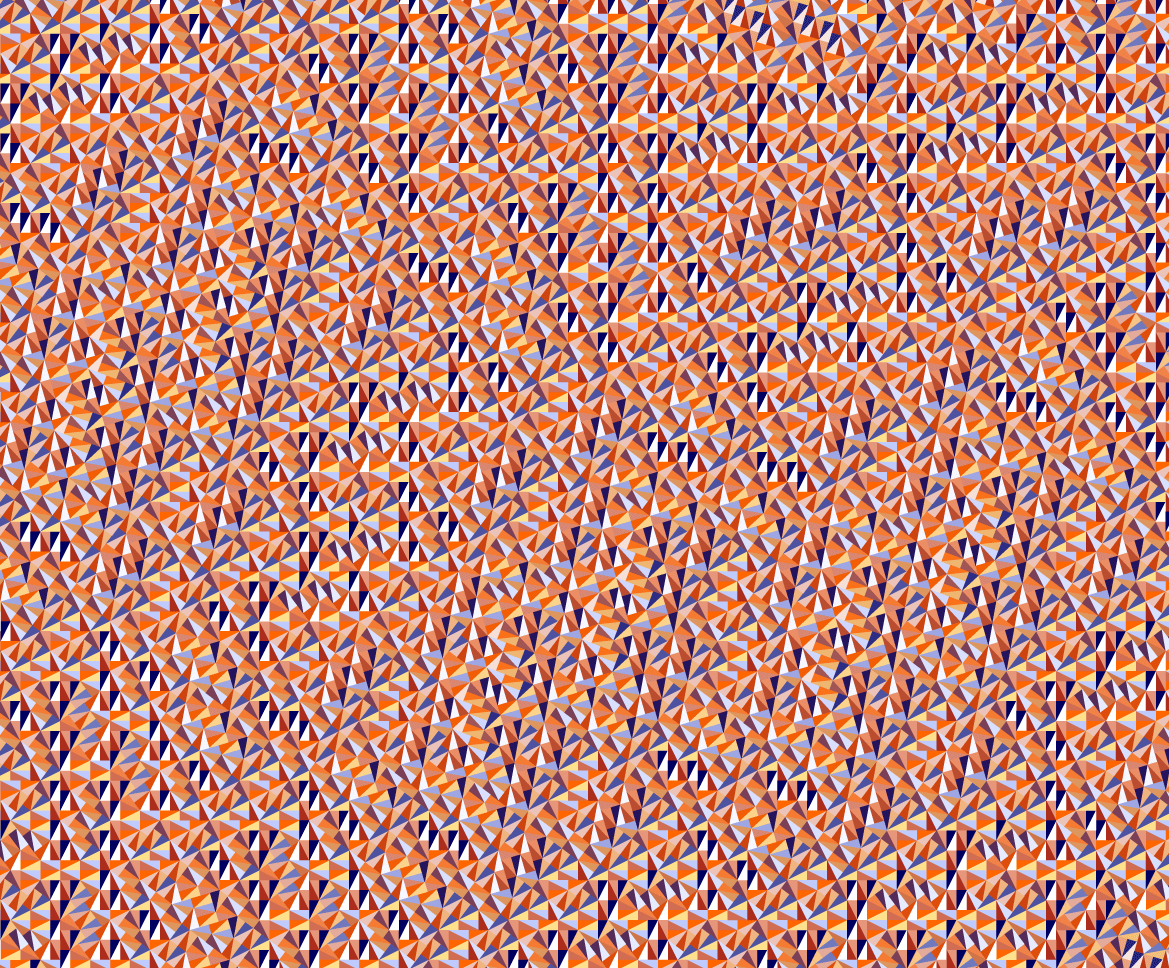
Patch Pinwheel

References

[Rad94]
Radin, C
The pinwheel tilings of the plane
Ann. of Math. (2) 1994, 139, 3, pp. 661--702, 95d:52021

[Rad97]
Radin, C
Aperiodic tilings, ergodic theory, and rotations
The mathematics of long-range aperiodic order, Kluwer Acad. Publ., Dordrecht 1997, NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 489, MR1460035

[Rad92]
Radin, C, Wolff, M
Space tilings and local isomorphism
Geom. Dedicata 1992, 42, 3, pp. 355--360, MR1164542