Square Chair

• Finite Rotations
• MLD Class Chair
• Parallelogram Tiles
• Polytopal Tiles
• Rhomb Tiles
• Self-Similar Substitution
• With Decoration
• p-adic Windowed Tiling

Info

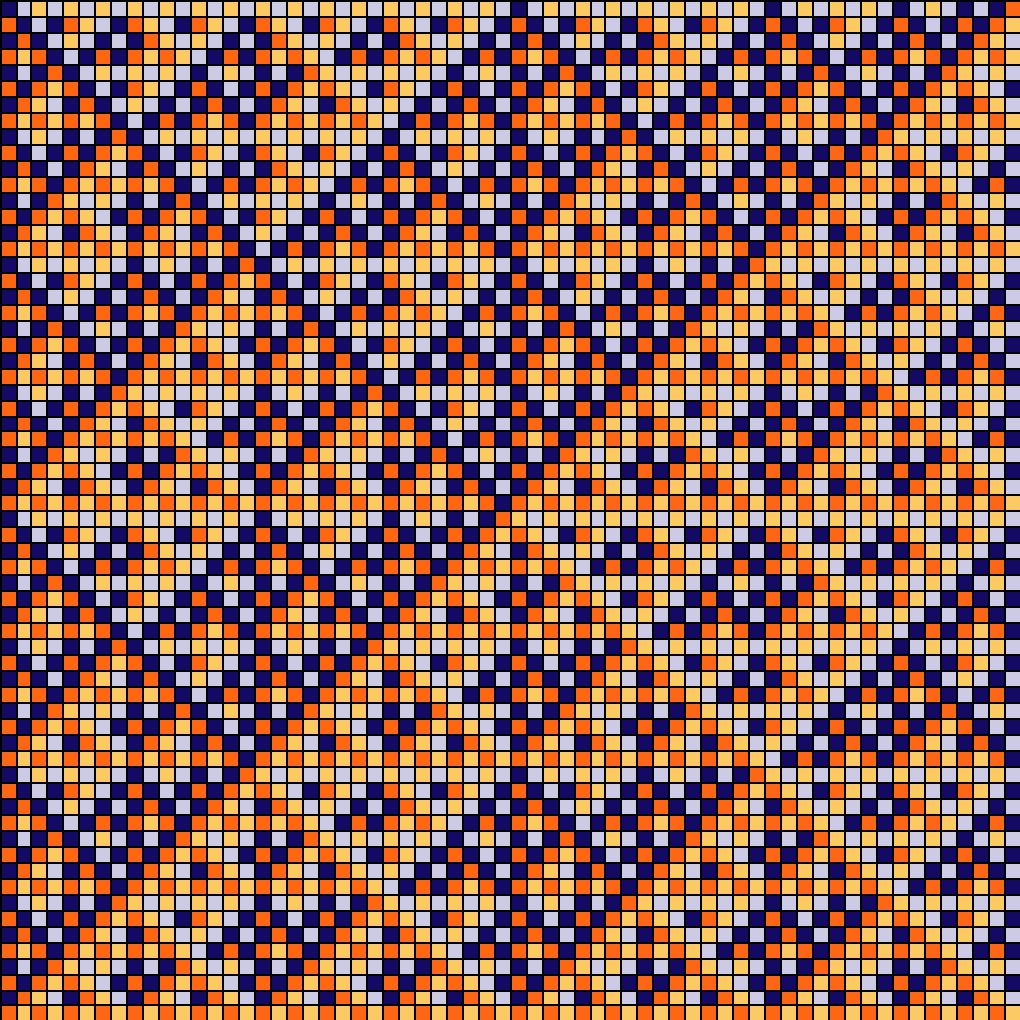
MLD to the more popular chair tiling, this version allows a simple translation into a coloured lattice: Replace each square of type i (1,2,3, or 4) with its midpoint, and assign to it colour i. Then each set of all points of colour i is a model set with internal p-adic space with p=2. This was first shown in [BMS98], a general framework is given in [LMS03].

Substitution Rule

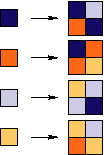
Patch

---

References

[BMS98]
Baake, M and Moody, R V and Schlottmann, M
Limit-(quasi-)periodic point sets as quasicrystals with p-adic internal spaces
J. Phys. A: Math. Gen. 1998, 31, pp. 55-65,

[LMS03]
Lee, J E S and Moody, R V and Solomyak, B
Consequences of Pure Point Diffraction Spectra for Multiset Substitution Systems
Discrete and Computational Geometry 2003, 29, pp. 525-560, MR1702375

---