Shield
- Euclidean Windowed Tiling
- Finite Rotations
- MLD Class Shield and Socolar
- Matching Rules
- Polytopal Tiles
- Polytopal Windowed Tiling
- With Decoration
Discovered by
Info
In connection with physical quasicrystals, the most interesting 2dim tilings are based on 5-, 8-, 10- and 12-fold rotational symmetry. This 12-fold tiling was studied by F. Gähler, in particular its cut and project scheme, the local matching rules and diffraction properties [Gah88]. The window of the vertex set of the shield It is mld to the Socolar tiling, thus they share many interesting properties. One is that they possess a local matching rules.
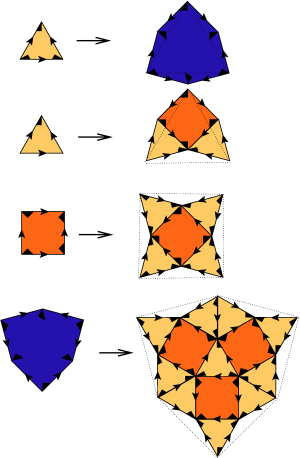
The local matching rule for the shield tiling is given by:
(a) tiles have to match edge-to-edge, such that the orientations given by the arrows match.
(b) the decorations of the tiles have to form a `cross’ at each vertex, which looks like the crosses at the three interior vertices in the rule image.
The decorations (arrows and cross parts) are shown in the rule image only, the patch image shows the shield tiling without these decorations.
Substitution Rule
Patch
References
[Gah88]
Gähler, F.
Crystallography of Dodecagonal Quasicrystals
Scientific
1988,