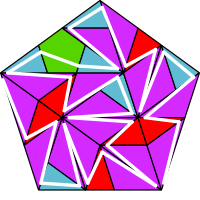
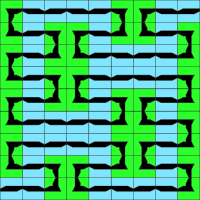
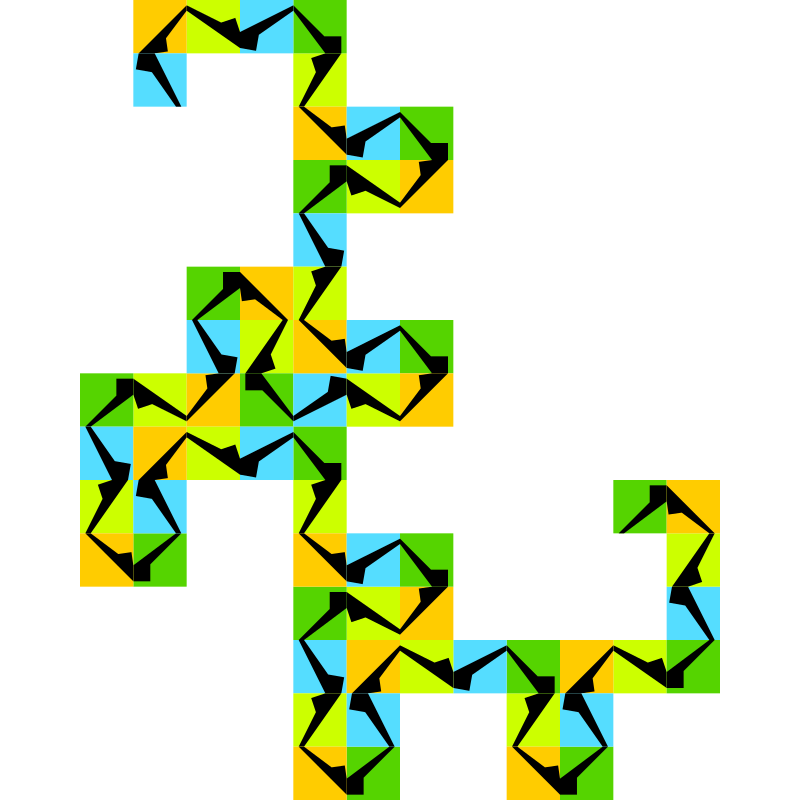FASS-curve

An FASS-curve is a curve which is space filling, self-avoiding, self-similar and simple. Simple means here that the curve can be drawn in one stroke. FASS-curves in the euclidean plane have a fractal dimension of D=2. As a consequence they can be derived from aperiodic substitution tilings by applying an appropriate decoration. The opposite way is also possible in many cases, so that curve and tiling form a dual structure.

Preview FASS-Curve of the Pentagon Substitution Tiling
FASS-Curve of the Pentagon Substitution Tiling

The FASS-curve of the pentagon bases on an aperiodic substitution tiling with four substitution rules and appropriate decorations. The substitution tiling was derived from the Robinson Triangle Tiling. Its inflation factor is the golden mean $\frac{\sqrt{5}}{2} + \frac{1}{2} = 1.618033988\ldots$.

Polytopal Tiles Self Similar Substitution With Decoration FASS_curve

Preview Gosper Curve Substitution Tiling
Gosper Curve Substitution Tiling

The Gosper Curve is a FASS-curve which can be derived by a substitution tiling with one substitution rule and appropriate decorations. The inflation factor $q$ is $sqrt(7)$.

Finite Local Complexity Polytopal Tiles Self Similar Substitution With Decoration Limitperiodic FASS_curve

Preview Heighway Dragon FASS-Curve Substitution Tiling
Heighway Dragon FASS-Curve Substitution Tiling

The original Heighway Dragon Curve as described in [gar1967] , can be derived by a substitution tiling with one substitution rule and appropriate decoration. However, it is not a FASS-curve because it is not self avoiding. With the results in [pau2021] it is possible to derive a substitution tiling which generates a Heighway Dragon FASS-Curve without disturbing self similarity. In detail the decoration on the proto tile is shifted away from the corners in different ways.

Finite Local Complexity Polytopal Tiles Self Similar Substitution With Decoration Limitperiodic FASS_curve

Preview Hilbert Curve Substitution Tiling
Hilbert Curve Substitution Tiling

The Hilbert Curve is one of the earliest FASS-curves. The original algorithm in [hil1891] bases on one substitution rule and an additional rule which describes how the substitutes have to be connected. As briefly mentioned in [pau2021] it is also possible to create the Hilbert Curve by a substitution tiling with two substitution rules and appropriate decorations. The inflation factor $q$ is 2 and the lines are shifted slightly away from the center of the sides to illustrate the matching rules.

Finite Local Complexity Polytopal Tiles Self Similar Substitution With Decoration Limitperiodic FASS_curve

Preview Peano Curve Substitution Tiling
Peano Curve Substitution Tiling

The Peano Curve is one the earliest known FASS-curves. The original algorithm in [pea1890] bases on one substitution rule and an additional rule which describes how the substitutes have to be connected. As briefly mentioned in [pau2021] it is also possible to create the Peano Curve by a substitution tiling with two substitution rules and appropriate decorations. The inflation factor $q$ is 3 and the lines are shifted slightly away from the center of the sides to illustrate the matching rules.

Finite Local Complexity Polytopal Tiles Self Similar Substitution With Decoration Limitperiodic FASS_curve