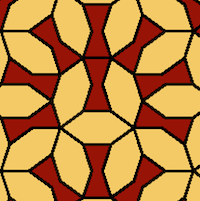
Girih
“Girih” is the Persian word for “knot” and stands for complex interlaced strap works of lines, which are a typical feature of Islamic architecture and design. A common definition is given in [All2004] :
“Geometric (often star-and-polygon) designs composed upon or generated from arrays of points from which construction lines radiate and at which they intersect.”
The oldest known examples of star pattern date back to the 8th century AD [Lee1987] . Girih designs are known in many styles and symmetries, see [Bou1973] for examples. A variant of Girih design relies on Girih tiles and tilings as shown in the reproduction of the Topkapi Scroll in [NA1995] . The decorations on the tiles consist of lines which run from tile to tile when they are joined together. So the borders between joined tiles seem to disappear.
It is possible to create aperiodic substitution tilings with prototiles in the shape of Girih tiles, as shown by E. Mackovicky by deriving aperiodic Girih tilings mld to the Penrose Pentagon boat star in [Mac1992] .
According to [NA1995] the shapes of all girih tiles (with dihedral symmetry ‘$D_{10}$’) are equilateral polygons with the same side length and inner angles ‘$\frac{k\pi}{5}$’, ‘$k\in\{2,3,4,6\}$’ including:
- Regular decagon with inner angles ‘$\frac{4\pi}{5}$’
- Regular pentagon with inner angles ‘$\frac{3\pi}{5}$’
- Rhomb with inner angles ‘$\frac{2\pi}{5}$’ and ‘$\frac{3\pi}{5}$’
- Convex hexagon with inner angles ‘$\frac{2\pi}{5}$’, ‘$\frac{4\pi}{5}$’, ‘$\frac{4\pi}{5}$’, ‘$\frac{2\pi}{5}$’, ‘$\frac{4\pi}{5}$’, ‘$\frac{4\pi}{5}$’
- Convex hexagon with inner angles ‘$\frac{3\pi}{5}$’, ‘$\frac{3\pi}{5}$’, ‘$\frac{4\pi}{5}$’, ‘$\frac{3\pi}{5}$’, ‘$\frac{3\pi}{5}$’, ‘$\frac{4\pi}{5}$’
- Nonconvex hexagon with inner angles ‘$\frac{2\pi}{5}$’, ‘$\frac{2\pi}{5}$’, ‘$\frac{6\pi}{5}$’, ‘$\frac{2\pi}{5}$’, ‘$\frac{2\pi}{5}$’, ‘$\frac{6\pi}{5}$’
The following definition turned out to be useful for aperiodic Girih substitution tilngs with other dihedral symmetry ‘$D_{2n}$’.
- All prototiles are equilateral polygons with the same side length.
- The inner angles of all prototiles are ‘$\frac{k\pi}{n}$’, ‘$k\in\left\{ 2,3...\left(n-1\right),\left(n+1\right),\left(n+2\right)...\left(n-2\right)\right\}$’.
- One of the prototiles may be a regular n-gon with inner angles ‘$\frac{\left(n-2\right)\pi}{n}$’.
- One of the prototiles may be a regular 2n-gon with inner angles ‘$\frac{\left(n-1\right)\pi}{n}$’.
- Prototiles with inner angle ‘$\frac{\pi}{n}$’ are excluded due to aesthetic reasons.
One of several substitution tilings found and submitted in February 2016 by L. Andritz with fivefold symmetry using tiles inspired by Islamic Girih patterns.
Despite the similarities the tiling is different to the “Tie and Navette” tiling as discussed in [Lue1990] and [LL1994] .
Finite Rotations Model Set Polytopal Tiles Self Similar Substitution Finite Local Complexity Girih
A tiling with fivefold symmetry using tiles inspired by Islamic Girih patterns.
Finite Rotations Polytopal Tiles Self Similar Substitution Finite Local Complexity Girih
One of several substitution tilings found by L. Andritz with fivefold symmetry using tiles inspired by Islamic Girih patterns.
Finite Rotations Polytopal Tiles Self Similar Substitution Finite Local Complexity Girih
One of several substitution tilings found by L. Andritz with fivefold symmetry using tiles inspired by Islamic Girih patterns.
Finite Rotations Polytopal Tiles Self Similar Substitution Finite Local Complexity Girih
The substitution tiling was derived from a mosaic at the Darb-i Imam Shrine in Isfahan, Iran. While the shrine dates back from 1453, [Lau2018] argues that the mosaic was created much later between 1715 - 1717.
The tiling relies on the regular decagon and two hexagons and has individual dihedral …
Finite Local Complexity Finite Rotations Polytopal Tiles Self Similar Substitution Girih
A tiling resembling Islamic Girih patterns but using 14-fold
symmetry rather than 8- or 10- or 12-fold.
Its inflation factor is $1 + \cos(\frac{\pi}{14}) \csc(\frac{\pi}{7}) + 2 \cos(\frac{3 \pi}{14}) \csc(\frac{\pi}{7}) = 6.850855...$
which is a unit but not a PV number.
It uses 11 prototiles …
Finite Local Complexity Finite Rotations Polytopal Tiles Self Similar Substitution Girih
References
[Mac1992]
Makovicky, E.
800-year-old pentagonal tiling from Maragha, Iran, and the new varieties of aperiodic tiling it inspired
Fivefold symmetry
1992,
67-86,
[Bou1973]
Bourgoin, J.
Arabic Geometrical Pattern and Design
1973,
[All2004]
Allen, T.
Islamic Art and the Argument from Academic Geometry
Solipsist Press: Occidental
2004,
http://www.sonic.net/~tallen/palmtree/academicgeometry.htm
[Lee1987]
Lee, A. J.
Islamic Art and the Argument from Academic Geometry
Muqarnas
1987,
4,
182–197,
https://doi.org/10.2307/1523103
[NA1995]
Necipoğlu, G.; Al-Asad, M.
The Topkapı Scroll: Geometry and Ornament in Islamic Architecture
1995,
https://www.getty.edu/publications/virtuallibrary/9780892363353.html