Infinity
Discovered by
Info
Denote the elements of the field $F_{4}$ by $\{0, 1, w, w + 1\}$, where $w$ satisfies the following equation with coefficients in $F_{2}: w^{2} + w + 1 = 0$.
Infinity is a recurrent double sequence defined by $a(i, 0) = a(0, j) = 1$ and $a(i, j) = f(a(i, j-1), a(i-1, j-1), a(i-1, j))$,
where $f(x, y, z) = x^{2} + (w + 1) y^{2} + z$.
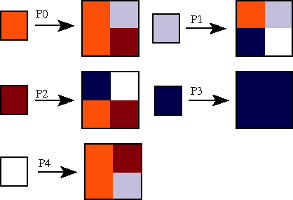
This recurrent double sequence can be also obtained using a system of substitutions of type 2 -> 4 with 5 rules.
What we present here are only the rules, renormed as system of substitutions of type 1 -> 2.
The 2 × 2 minors appearing in the double sequences in even positions are replaced by simple squares,
introducing for every of the 5 occurring 2 $\times$ 2 minor a new color.
The system of substitutions of type 1 -> 2 got this way is called skeleton of the original system of substitutions.
What you see here is “the skeleton of Infinity”.
Substitution Rule
Patch
download vectorformat Infinity