Mothman

Info

Denote the elements of the field $F_{4}$ by $\{0, 1, w, w + 1\}$, where $w$ satisfies the following equation with coefficients in $F_{2}: w^{2} + w + 1 = 0$. Mothman is a recurrent double sequence defined by $a(i, 0) = a(0, j) = 1$ and $a(i, j) = f(a(i, j-1), a(i-1, j-1), a(i-1, j))$, where $f(x, y, z) = x^{2} + (w + 1) y^{2} + z^{2}$. This recurrent double sequence can be also obtained using a system of substitutions of type 2 -> 4 with 15 rules, as it follows.

Substitution Rule

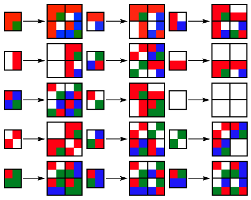
Patch

---