Ammann-Beenker

Discovered by

Info

In 1977 R. Ammann found several sets of aperiodic tiles. This one (his set A5) is certainly the best-known of those. It allows tilings with perfect 8fold symmetry. The substitution factor is $1+\sqrt{2}$ - sometimes called the ‘silver mean’ - which was the first irrational inflation factor known which is not related to the golden mean. In 1982 F. Beenker described their algebraic properties, essentially how to obtain it by the projection method, following the lines of N. G. deBruijn (see [Bee82] , [de81] ). As in the Penrose Rhomb tiling, these tiles allow a decoration by so called Ammann bars (see [GS87] , or [Luc93] and references therein). That means, the two prototiles can be decorated with line segments, such that this segments extend to biinfinite straight lines throughout the tiling(building the ‘Ammann grid’). There is even a decoration by such lines which forces the local matching rule, but to achieve this, the lines has to extend beyond the boundary of the prototiles (J. Socolars ‘secondary Ammannlines’, see [Soc89] ). Another interesting property is the appearance of ‘Conway worms’ (see [Soc89] , or [GS87] for the Penrose case). That means, there are arbitrary long sequences of tiles, extending along a line and obeying a one dimensional substitution rule. In this case, one such rule is given by $r \to R$ , $R \to RrR$, where R is the long diagonal of a rhomb, r the short one. One can find such sequences in the picture below. One of those starts exactly in the upper left corner of the picture, following a line which is descending with a slope of $\frac{\pi}{8}$ ($22.5^{\circ}$ ). There is another kind of worm, built by squares and hexagons (each hexagon consisting of two rhombs and a square), the according rule is $S \to SH$, $H \to SSH$.

Substitution Rule

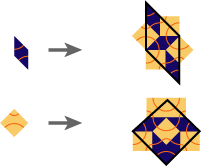
Rule Ammann-Beenker

Patch

Patch Ammann-Beenker

References

[de81]
de Bruijn, N G
Algebraic theory of Penrose's nonperiodic tilings of the plane. I, II
Nederl. Akad. Wetensch. Indag. Math. 1981, 43, no. 1, 39-52, 53-66, 82e:05055

[Bee82]
Beenker, F P M
Algebraic theory of non-periodic tilings of the plane by two simple building blocks: a square and a rhombus
Eindhoven University of Technology 1982, TH-Report, 82-WSK04

[Luc93]
Lück, R
Basic ideas of Ammann bar grids
Int. J. Mod. Phys. B 1993, 7, pp. 1437-53, MR1215343

[Soc89]
Socolar, J E S
Simple octagonal and dodecagonal quasicrystals
Phys. Rev. B 1989, 39, pp. 10519-10551, MR0998533

[GS87]
Grünbaum, B and Shephard, G.C.
Tilings and Patterns
W.H. Freeman 1987, MR0857454