Cyclotomic Trapezoids 7-fold
Discovered by
Info
In order to generalize Danzer’s 7-fold tiling to n-fold symmetry,
where n>5 is odd, L. Danzer and D. Frettlöh introduced trapezoidal tiles,
each one the union of two triangles with edge lengths of the form $\sin(k \frac{\pi}{n})$.
It needs some further effort, including the introduction of three additional prototiles (two pentagons, one non-trapezoidal quadrangle),
but one obtains an infinite series of substitution rules based on n-fold symmetry (n odd).
Unfortunately, none of these tilings show perfect n-fold symmetry, as Danzer’s 7-fold does,
thus loosing aesthetic appeal.
Substitution Rule
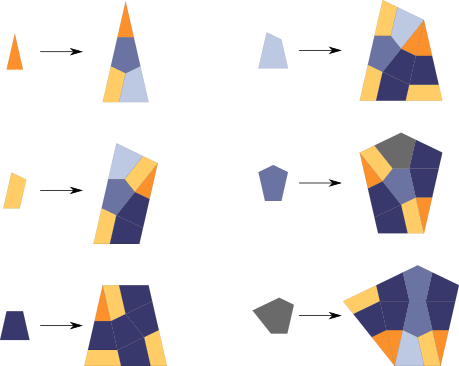
Patch
download vectorformat Cyclotomic Trapezoids 7-fold