Danzer's 7-fold
Discovered by
Info
A substitution tiling with three triangles as prototiles,
based on 7-fold symmetry.
The four different edge lengths occurring are $\sin(\frac{\pi}{7})$, $\sin(\frac{2\pi}{7})$,
$\sin(\frac{3\pi}{7})$, $\sin(\frac{2\pi}{7}) + \sin(\frac{3\pi}{7})$,
The inflation factor is $1+{\sin(\frac{2\pi}{7})}/{\sin(\frac{\pi}{7})}$
, which is not a PV number.
There are simple matching rules for the tiling. In fact, the list of all vertex stars occurring in the substitution tiling serves as one. This is stated in [ND96], but never really published, up to my knowledge. The mentioned paper focusses on different tilings.
Find the vector graphic here.
Substitution Rule
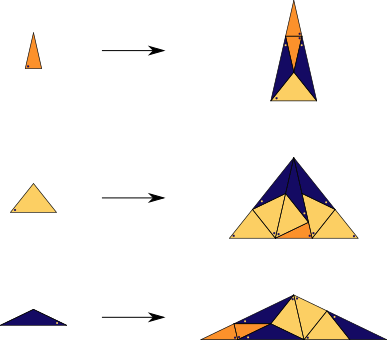
Patch
download vectorformat Danzer's 7-fold
References
[ND96]
Nischke, K-P and Danzer, L
A construction of inflation rules based on $n$-fold symmetry
Discrete and Computational Geometry
1996,
15,2,
pp. 221-236,
96j:52035