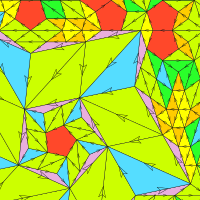
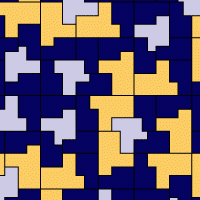
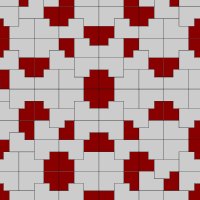
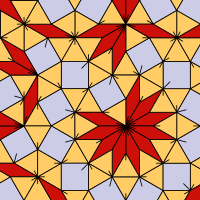
Self-Similar Substitution
A substitution (at least here) consists of rules how to enlarge a tile and replace the enlarged tile with other tiles. If the union of the latter ones is similar to the original tile, then the substitution is called self-similar substitution. For example, the substitution for the Penrose Rhombs is not self-similar, but the substitution for the Robinson Triangles is.
In other words, a substitution is a self-similar substitution, if $\sigma(T)=T$. A substitution tiling is called self-similar, if it can be generated by a self-similar substitution. It is known that any - sufficiently nice, i.e., repetitive and flc wrt translations - tile substitution in the plane can be made self-similar, by using fractal boundaries.
A weaker version is described by the term ‘self-affine’ tiling [LW96] , [BG94] . The definition of this reads exactly as above if one replaces ‘similar to’ with ‘affine image of’.
References
[BG94]
Bandt, C and Gelbrich, G
Classification of self-affine lattice tilings
J. London Math. Soc.
1994,
50,
pp. 581-593,
[LW96]
Lagarias, J C and Wang, Y
Self-affine tiles in $\mathbb{R}^n$
Adv. Math.
1996,
121,
pp. 21-49,
MR1399601