Tuebingen Triangle
Discovered by
Info
Beside the Penrose rhomb tilings (and its variations), this is a classical candidate to model 5-fold (resp. 10-fold) quasicrystals. The inflation factor is - as in the Penrose case - the golden mean, $\frac{\sqrt{5}}{2} + \frac{1}{2}$. The prototiles are Robinson triangles, but these tilings are not mld to the Penrose tilings. The relation is different: The Penrose rhomb tilings are locally derivable from the Tübingen Triangle tilings.
These tilings were discovered and studied thoroughly by a group in Tübingen, Germany, thus the name [BKSZ90]
.
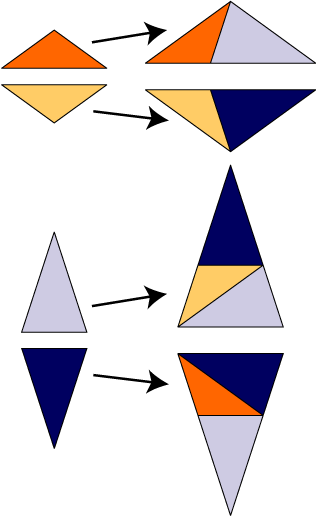
Since the prototiles are mirror symmetric, but their substitutions are not, we have to distinct left-handed and right-handed tiles. This is indicated by the colours in the substitution rule and in the patch below.
Substitution Rule
Patch

References
[BKSZ90]
Baake, M and Kramer, P and Schlottmann, M and Zeidler, D
Planar patterns with fivefold symmetry as sections of periodic structures in $4$-space
Internat. J. Modern Phys. B
1990,
4, 15-16,
pp. 2217--2268,
92b:52041