Penrose Rhomb

Discovered by

Info

Certainly the most popular substitution tilings. Discovered in 1973 and 1974 by R. Penrose in - at least - three versions (Rhomb, Penrose kite-dart and Penrose Pentagon boat star), all of them forcing nonperiodic tilings by matching rules. It turns out that the three versions are strongly related: All three generate the same mld-class. These tiles, their matching rules and the corresponding substitution was studied thoroughly in [GS87] . A lot of information can be found there. The matching rule for the Penrose rhomb tiling is rather simple: Either the set of vertex stars of the undecorated tiling can serve as the rule. Or, using the red arcs shown in the rule here, the matching rule is given by the condition that tiles have to meet in a way such that the arcs of each tile is connected with arcs on the neighboured tiles.

The inflation factor is the golden mean $\frac{\sqrt{5}}{2} + \frac{1}{2} = 1.618033988\ldots$, and the tiling is strongly related with Fibonacci numbers and the Fibonacci sequence. For instance, all entries in the powers of the substitution matrix are Fibonacci numbers. Or, the distances of Ammann bars in the Penrose tilings are ordered like a Fibonacci sequence. Or, there are ‘Conway worms’ made of fat and thin hexagons, ordered like a Fibonacci sequence. The Penrose tilings are patented, U.S. Patent 4133152.

deBruijn showed in [de81] how to obtain the Penrose tilings by projecting certain lattice points from higher dimensions. This was the starting point of the theory of cut and project tilings. A lot of literature is devoted to this topic. A controversal question arising for the Penrose tilings was: What is the right choice for the internal space, better: What is the ‘minimal embedding’? A typical choice is $\mathbb{R}^3$, using the primitive lattice $\mathbb{Z}^5$. But it is also possible using $\mathbb{R}^2$, together with the root lattice $A_4$ [BKSZ90] . Another possibility is $\mathbb{R}^2 \times C_5$ [BM04] .

Substitution Rule

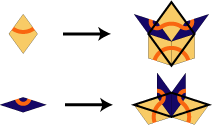
Rule Penrose Rhomb

Patch

Patch Penrose Rhomb

References

[BM04]
Baake, M and Moody, R V
Weighted Dirac combs with pure point diffraction
J. Reine Angew. Math. 2004, 573, pp. 61-94, MR2084582

[BKSZ90]
Baake, M and Kramer, P and Schlottmann, M and Zeidler, D
Planar patterns with fivefold symmetry as sections of periodic structures in $4$-space
Internat. J. Modern Phys. B 1990, 4, 15-16, pp. 2217--2268, 92b:52041

[de81]
de Bruijn, N G
Algebraic theory of Penrose's nonperiodic tilings of the plane. I, II
Nederl. Akad. Wetensch. Indag. Math. 1981, 43, no. 1, 39-52, 53-66, 82e:05055

[GS87]
Grünbaum, B and Shephard, G.C.
Tilings and Patterns
W.H. Freeman 1987, MR0857454