Danzer's non-FLC 5
Discovered by
Info
Part of an infinite series of triangle susbstitutions described by L.Danzer. Most of them are not flc, this one being one of the simplest examples in this series. The substitution factor is of algebraic degree 5. The positions where one can ‘see’ the non-flc property are fault-lines throughout the tiling where the tiles don’t meet vertex-to-vertex. One of these fault lines is visible in the picture, it is located near the diagonal of the image. In the center, two light brown triangles meet vertex-to-vertex. Apart from that, the tiles meet in many different ways along the fault-line. One can show that there are infinitely many ways how they meet along an infinite fault-line.
Substitution Rule
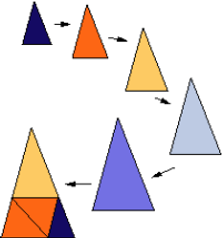
Patch
