Kenyon's non FLC (volume hierarchic)

Discovered by

Info

A simple substitution rule, generating tilings which don’t possess flc. The fractally shaped tiles make it a selfsimilar-substitution. Despite the fractal apperance, the dimension of the boundary of the prototile is one almost everywhere: the boundary of the tile consists of lines almost everywhere (plus accumulation points). Unlike the Koch curve, for instance, or the fractal Dart and Kite prototiles, here the entire length of the boundary is finite. For more details, see Kenyon non-FLC.

Substitution Rule

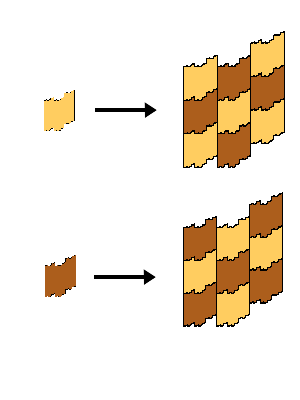
Rule Kenyon's non FLC (volume hierarchic)

Patch

Patch Kenyon's non FLC (volume hierarchic)