Say-awen 17-fold

Discovered by

Info

A substitution rule that gives rise to a non-periodic tiling $\mathcal{T}{17}$ with $17$-fold dihedral symmetry. The substitution factor is $\mu{17}=1/(2\sin(\pi/34))$.

The tiling $\mathcal{T}{17}$ is obtained by assigning orientations to relevant tiles in the 1-order supertiles to ensure the existence of a patch invariant under $17$-fold dihedral symmetry in a supertile of the substitution. This patch of $34$ triangles equivalent to $T{17,15}$ whose $\pi/17$ vertices meet at a point serves as the seed for $\mathcal{T}_{17}$.

Moreover, the tiling $\mathcal{T}{17}$ has infinite local complexity (or is non-FLC). The proof of the non-FLC property is based on an algorithm by Danzer, which makes use of the fact that $\mu{17}$ is non-Pisot. The minimal polynomial of $\mu{17}$ is $p{17}(x)=x^8-4x^7-10x^6+10x^5+15x^4-6x^3-7x^2+x+1$.

Substitution Rule

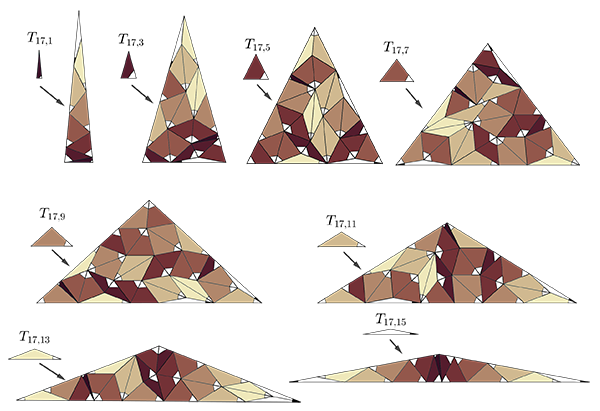
Rule Say-awen 17-fold

Patch

Patch Say-awen 17-fold download vectorformat Say-awen 17-fold

References

[Say2024]
Say-awen, A. L. D.
Tilings with Infinite Local Complexity and n-Fold Rotational Symmetry, n=13,17,21
arXiv 2024, https://doi.org/10.48550/arXiv.2408.17082