Fibonacci Times Fibonacci
- Euclidean Windowed Tiling
- Finite Rotations
- Parallelogram Tiles
- Polytopal Tiles
- Polytopal Windowed Tiling
- Rhomb Tiles
- Self-Similar Substitution
Info
The 2dim analogue of the famous Fibonacci tiling in one dimension.
It is just the Cartesian product of two Fibonacci tilings $F_{1}$, $ F_{2} : \{ T_{1} \times T_{2}\ |\ T_{i}\ in\ F_{i}\}$.
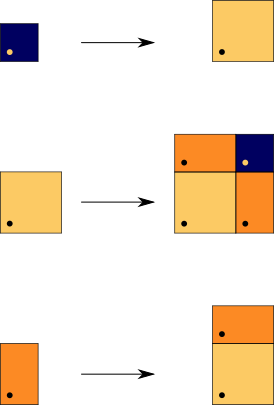
Obviously, it can be generated by a substitution with three prototiles.
It shares a lot of nice features with the 1dim Fibonacci tiling:
It is a model set (better: it’s mld with one), so it has pure point spectrum.
Its window is just a square. Moreover, it is its own dual tiling.
Trivially, it allows a decoration with Ammann bars.
Substitution Rule
Patch
download vectorformat Fibonacci Times Fibonacci