Chaim's Cubic PV

• Euclidean Windowed Tiling
• Finite Rotations
• Polytopal Tiles
• Self-Similar Substitution

Info

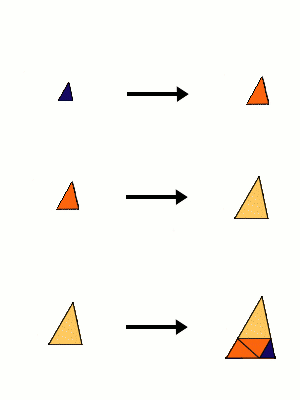
Part of an infinite series, where most tilings in this series are not flc, this one is the exception. The reason is that the inflation factor is a - real - PV number. By an argument in [PR] this forces flc. Interestingly, the shape of the tiles can vary. That is, there is one free parameter $l$ , $0 < l < 1+s$, and the smallest prototile is the triangle with sides $1,s,l$ ($s$ the largest root of $x^{3}-x-1$). In particular, one can have obtuse triangles, as well as rectangular ones or acute ones as prototiles.

Substitution Rule

Patch

---

References

[PR]
Priebe-Frank, N and Robinson, E A jr
Generalized beta-expansions, substitution tilings, and local finiteness
preprint A0506098

---