Chord Quadrangle 3-3
Discovered by
Info
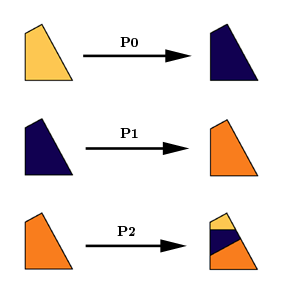
A member of an infinite family of substitution rules for similar quadrangles possessing two right interior angles at opposite vertices. A big copy of such a quadrangle can be divided into (smaller) similar quadrangles in several ways. Some of them are compatible with a substitution rule. This one is the smallest possibility, using three prototiles. Examples with more prototiles are Chord-Quadrangle-4-3, Chord-Quadrangle-5-3, Chord-Quadrangle-5-5, and so on. (Search for chord-quadrangle.)
Substitution Rule
Patch
