Conch

Discovered by

Info

This tiling and Nautilus are dual tilings generated by non-PV morphisms. As such they are the first step in a generalisation of the work of G. Rauzy, P. Arnoux, S. Ito and others for PV substitution rules. The work that developed out of G. Rauzy’s seminal paper [Rau82] .

The inflation factor for this substitution rule is either of the expanding roots of: $x^{4}-x+1 = 0$. Note that this it is related to R. Kenyon’s example Kenyon 2 that is shown on his homepage: http://www.math.brown.edu/~rkenyon/gallery/gallery.html and has inflation factor satisfying $x^{4}-x+1 = 0$.

Conch (Volume Hierarchic) is a volume hierarchic, version of this substitution rule with fractal bounded tiles.

Substitution Rule

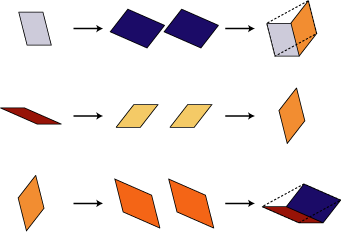
Rule Conch

Patch

Patch Conch

References

[Rau82]
Rauzy, G
Nombres algébriques et substitutions (French) [Algebraic numbers and substitutions]
Bull. Soc. Math. France 1982, 110, 2, pp. 147-178, MR0667748