Hexagonal Aperiodic Monotile
Discovered by
Info
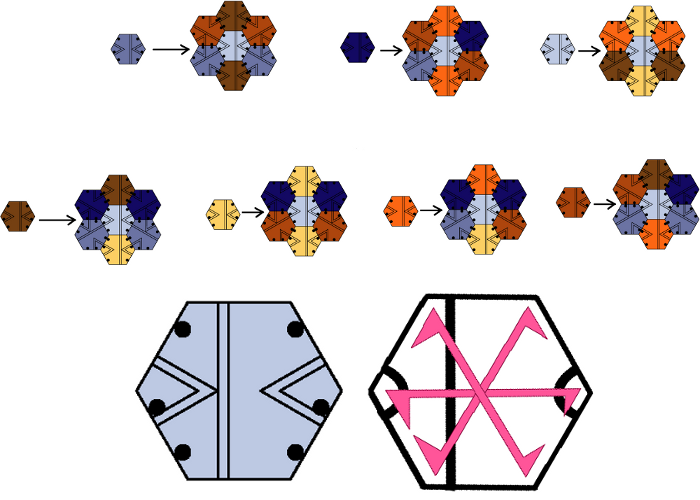
In 2009 Joan Taylor (Burnie, Tasmania) found a decoration of the hexagon, which - together with few local matching rules - allows only aperiodic tilings of the plane. This was probably the best example of an aperiodic monotile before the discovery of the Hat tiling. This decorated hexagonal tile, together with the local matching rule, is shown in Fig 1 of a joint paper by J. Socolar and J. Taylor: http://arxiv.org/pdf/1003.4279v2. It contains also a non-decorated version of the prototile, but then the prototile is not longer a simply connected set. (There is a non-connected version and a connected version with cut-points). This paper contains also a substitution rule yielding the same tilings as the local matching rule. A slightly different version of this substitution rule is shown here. This is not longer a proper self-similar substitution. It uses 7 hexagonal prototiles (Taylor uses 14 half-hex tiles, making the substitution self-similar). The 7 prototiles are distinguished by colour here. If we generate a (large patch of) a tiling using the substitution, and then delete all colours, we get the same tilings as the ones generated by the local matching rule (in the stricter version of the manuscript cited below). The above image on the left shows the substitution rule for the 7 prototiles, and below the original decoration of Socolar and Taylor (right) and our humble version of it. A manuscript by Joan Taylor with hand-drawn images can be found at https://sfb701.math.uni-bielefeld.de/preprints/sfb10015.pdf
Substitution Rule
Patch
