Hofstetter-4fold (plain)
Discovered by
Info
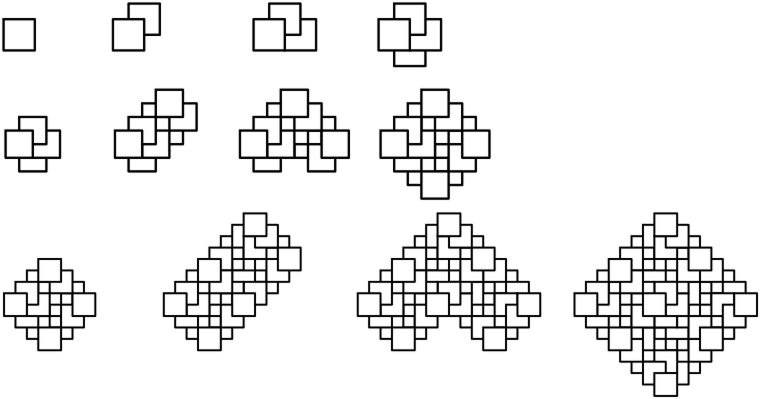
The Viennese Artist Hofstetter Kurt found a new iteration method that produces aperiodic tilings. The idea is illustrated in the figure below: one starts with a single square tile of edge length one. A second square tile of the same size is put below the first one, such that its SW corner is located at the midpoint of the first one. (The idea is that the first tile covers a part of the second tile.) Then a third tile is put below the second one, such that it’s NW corner is located at the centre of the second tile. A fourth tile is then put (partly) below the others as indicated.
Now we repeat the construction with copies of this first generation patch on a larger scale: place four copies of the first patch in a similar manner as above, where every distance is now doubled. This yields a second generation patch with 16 squares altogether. Four copies of this 2nd generation patch yield the 3rd generation patch and so on.
This construction can be applied to undecorated squares, but the squares can as well be equipped with a decoration. It was shown in [FH15] that a decorated version of the resulting tilings, the Hofstetter arrow tilings, are mld to a certain proper substitution tiling. Using this it was shown that the arrow tilings are indeed aperiodic, as well as limitperiodic. We believe (but haven’t proven yet) that the same is true for the undecorated tiling shown here.
Hofstetter Kurt generated several artistic versions of these tilings, using distinct decorations of the prototile. One is shown under Hofstetter 4fold (decorated).
There are also 3-fold and 6-fold variants of this construction. Artistic versions of these are Hofstetter 3fold tilings and Hofstetter 6fold tilings.
Substitution Rule
Patch

References
[FH]
Frettlöh, D and Hofstetter, K
Inductive rotation tilings
Proc. Steklov Inst. Math.
2015,
288,
pp. 247-258,