Square-triangle
Discovered by
Info
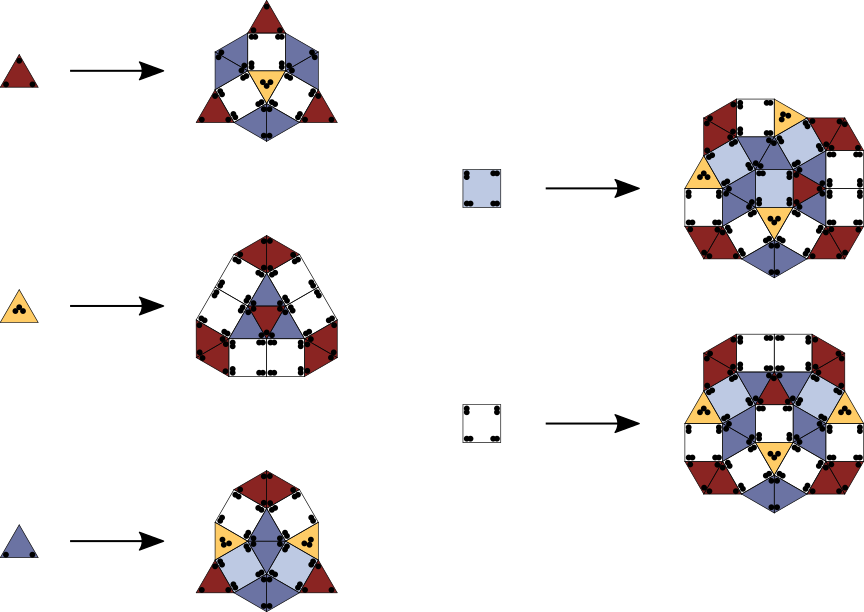
The substitution tilings which are most relevant as models for physical quasicrystals are 5-fold, 8-fold, 10-fold and 12-fold symmetric ones. In the 5-fold (resp. 10-fold) case, there are the variations of the Penrose rhomb tilings and the Tuebingen triangle, for the 8-fold case there are the Ammann-Beenker tilings. These examples use a minimal set of prototiles, in the sense that the number of prototiles is equal to the algebraic degree of the corresponding inflation factor. (The number of prototiles cannot be smaller than the algebraic degree.) Prominent examples of 12-fold tilings are the shield and the Socolar tilings. These are not minimal in the above sense; both of them use three prototiles. Here is a 12-fold tiling with (cum grano salis) only two prototiles, a square and a triangle. To be precise: It uses five prototiles, two squares and three triangles, which allow a substitution. If one forgets the markings of the tiles in the generated tilings, one obtains 12-fold tilings with only two types of tiles: square and triangle. This rule is given in [HM97].
It is conjectured that each 12-fold square triangle tiling which is a cut and project tiling has a fractal window.
The window of a square triangle tiling (I am not sure whether it is this one) is shown in [Baa98].
Most interestingly, this window is a fundamental domain of the hexagonal lattice,
even though it has 12-fold dihedral symmetry!
Substitution Rule
Patch
download vectorformat Square-triangle
References
[BaakeMS98]
Baake, M and Moody, R V and Schlottmann, M
Limit-(quasi) periodic point sets as quasicrystals with p-adic internal spaces
Journal of Physics A: Mathematical and General
1998,
31(27),
pp. 55-65,
arxiv.9901008
[HM97]
Hermisson J, Richard C and Baake M
A guide to the symmetry structure of quasiperiodic tiling classes
J. Physique I
1997,
7,
pp. 1003-18,
MR1474429