Ammann A3
- Euclidean Windowed Tiling
- Finite Rotations
- Polytopal Tiles
- Self-Similar Substitution
- Without Decoration
Discovered by
Info
In 1977 Robert Ammann discovered a number of sets of aperiodic prototiles, i.e., prototiles with matching rules forcing nonperiodic tilings. These were published as late as 1987 in [GS87] , where they were named Ammann A2 (our Ammann Chair), Ammann A3, Ammann A4 and Ammann A5 (better known as Ammann Beenker tiling). The substitution of this one uses the golden ratio as inflation factor. It is certainly true that this is a cut and project tiling, but to our knowledge, noone bothered to compute the window of it up to now. So we don’t know whether it is polytopal or not.
Substitution Rule
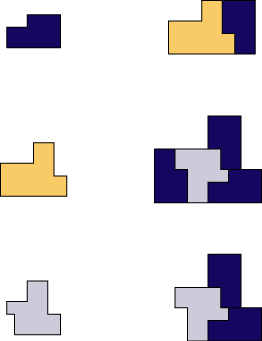
Patch

References
[GS87]
Grünbaum, B and Shephard, G.C.
Tilings and Patterns
W.H. Freeman
1987,
MR0857454