Godreche-Lancon-Billard Binary

Discovered by

Info

In [Lan88], energetic properties of certain decorations of Penrose Rhomb tilings were studied. A binary tiling was defined as a tiling by Penrose rhombs, where at each vertex all angles are either in {$\frac{\pi}{5}$, $3\frac{\pi}{5}$}, or in {$2\frac{\pi}{5}$, $4\frac{\pi}{5}$}. (‘Binary’ because the decorations were used to model binary alloys, i.e., alloys consisisting of two metallic elements). The authors did not mention the substitution rule explicitly, but it is obvious from the diagrams in this paper.

As a substitution tiling, the binary tiling is mentioned in [GoLa92], as a tiling with the 5-fold rhombs, and a non-PV inflation factor.

In contrast to the Penrose Rhomb tilings, these binary tilings do not obey the alternation condition. For an edge-to-edge rhomb tiling, the alternation condition reads: Start with an arbitrary edge of some tile $T_{0}$. Let $T_{1}$ be the tile sharing this edge with $T_{0}$. Go over to the opposite edge of $T_{1}$ which is parallel to the first edge. Let $T_{2}$ be the tile sharing the new edge with $T_{1}$. Proceed in this manner to obtain a sequence of tiles. (And now, the condition:) Whenever two tiles of the same type in such a sequence are adjacent, or separated by tiles of different type only, they are mirror images of each other. One can see in the image that the alternation condition does not hold for the binary tiling.

Substitution Rule

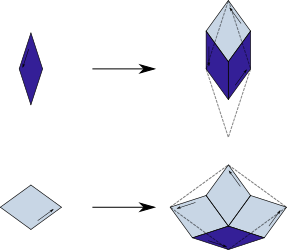
Rule Godreche-Lancon-Billard Binary

Patch

Patch Godreche-Lancon-Billard Binary download vectorformat Godreche-Lancon-Billard Binary

References

[GoLa92]
Godrèche, C., Lançon, F.
A simple example of a non-Pisot tiling with five-fold symmetry
J. Physique I 1992, 2, pp. 207-220, MR1185612

[Lan88]
Lançon, F, Billard, L.
Two-dimensional system with a quasicrystalline ground state.
J. Physique 1988, 49, 2, pp. 249-256, MR0933982