Danzer's 7-fold original
Discovered by
Info
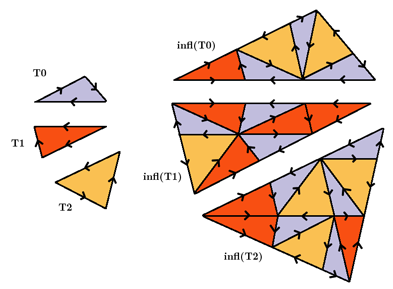
A tiling based on 7-fold (resp. 14-fold) symmetry [ND96].
The inflation factor is $1+{\sin(\frac{2\pi}{7})}/{\sin(\frac{\pi}{7})}$.
The three different edge lengths are proportional to
$\sin(\frac{\pi}{7})$, $\sin(\frac{2\pi}{7})$,
$\sin(\frac{3\pi}{7})$.
On a first glance, there seems to exist a centre of perfect 14-fold symmetry:
a 14-tipped star in the upper right corner.
But in fact it is only 2-fold symmetric.
The symmetry is broken by the right- and left-handedness of the tiles.
On rings around the 14-tipped star, this manifests in tiles pointing clockwise or counterclockwise, thus breaking the symmetry.
This is one of the rare cases that a substitution has local matching rules without decoration. In fact, the list of all different vertex stars defines the matching rule.
Substitution Rule
Patch

References
[ND96]
Nischke, K-P and Danzer, L
A construction of inflation rules based on $n$-fold symmetry
Discrete and Computational Geometry
1996,
15,2,
pp. 221-236,
96j:52035