Domino variant
- Finite Rotations
- Parallelogram Tiles
- Polyomio Tiling
- Polytopal Tiles
- Rep-Tiles
- Self-Similar Substitution
- p-adic Windowed Tiling
Info
A simple variant of the domino tilings (aka table tilings).
C. Goodman-Strauss pointed out in [Goo98] the following. B. Solomyak
proved in Sol98,
that for each nonperiodic substitution tiling the substitution rule is invertible:
One can tell from $\sigma(T)$ its predecessor $T$ uniquely. But this is true only if the prototiles have the same symmetry group as the first order supertiles.
By using decorated tiles this can always be achieved. (And now Chaims remark:) Here we see a case where such a decoration is necessary.
In the tiling with unmarked tiles shown below one cannot determine the supertiles uniquely.
By using the marks shown in the rule above the disambiguity vanishes.
Substitution Rule
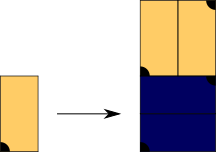
Patch
download vectorformat Domino variant
References
[Goo98]
Goodman-Strauss, Chaim
Matching rules and substitution tilings
Ann. of Math. (2)
1998,
147, 1,
pp. 181--223,
MR1609510
[Rob99]
Robinson, E. Arthur, Jr.
On the table and the chair
Indag. Math. (N.S.)
1999,
10, 4,
pp. 581--599,
MR1820555