Generalized Godreche-Lancon-Billard Binary

• Finite Local Complexity
• Finite Rotations
• Polytopal Tiles
• Rhomb Tiles

Info

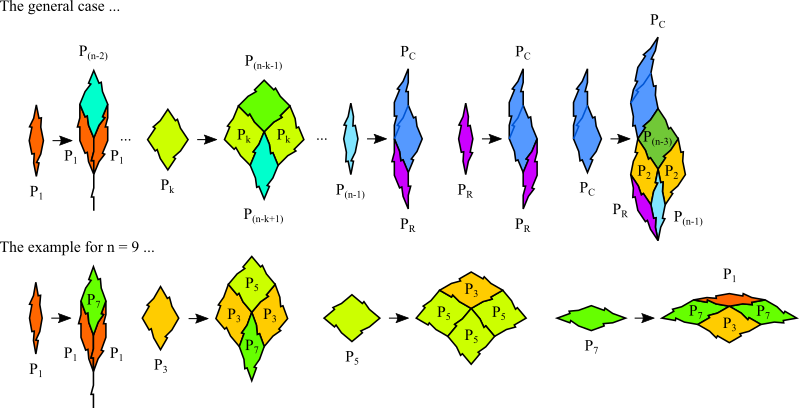
This tiling is a generalization of the Godreche-Lancon-Billard Binary first derived by T. Hibma and later worked out in detail by S. Pautze. All interior angles are integer multiples of $\frac{\pi}{n}$. For $n=5$ it is identical to the Godreche-Lancon-Billard Binary tiling with 2 prototiles. For odd $n$ it has $\frac{n-1}{2}$ prototiles. For even $n$ it has $n+1$ prototiles. The inflation multiplier is $\sqrt{2 + 2 \cos(\frac{\pi}{n})}$. The example shown below is the tiling for $n=9$.

Substitution Rule

Patch

download vectorformat Generalized Godreche-Lancon-Billard Binary

---

References

[Pau2017]
Pautze, S
Cyclotomic aperiodic substitution tilings
Symmetry 2017, 9(2), doi.org/10.3390/sym9020019

[Hib2015]
T. Hibma
Generalization of Non-periodic Rhomb Substitution Tilings
arXiv 2015, https://arxiv.org/abs/1509.02053

---