Infinite Number of Prototiles

• One Dimensional
• Self-Similar Substitution

Info

An one-dimensional substitution rule that uses an infinite number of prototiles.

The inflation factor is $2.5$.

The substitution rules are given by:

$T_{0}\rightarrow T_{0},T_{1}$

$T_{1}\rightarrow T_{0},T_{0},T_{2}$

$T_{2}\rightarrow T_{0},T_{1},T_{3}$

$T_{k}\rightarrow T_{0},T_{k-1},T_{k+1}$

$T_{\infty}\rightarrow T_{0},T_{\infty},T_{\infty}$

The corresponding substitution matrix can be written as:

$1 2 1 1 1 1 1 1 1 ...$

$1 0 1 0 0 0 0 0 0 ...$

$0 1 0 1 0 0 0 0 0 ...$

$0 0 1 0 1 0 0 0 0 ...$

$0 0 0 1 0 1 0 0 0 ...$

$0 0 0 0 1 0 1 0 0 ...$

$0 0 0 0 0 1 0 1 0 ...$

$0 0 0 0 0 0 1 0 1 ...$

$0 0 0 0 0 0 0 1 0 ...$

$...$

The lengths of the proto tiles are given by:

$length(T_{0})=1$

$length(T_{1})=\frac{3}{2}$

$length(T_{2})=\frac{7}{4}$

$length(T_{k})=\frac{2^{k+1}-1}{2^{k}}$

$length(T_{\infty})=2$

Substitution Rule

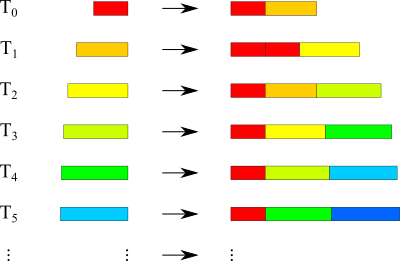
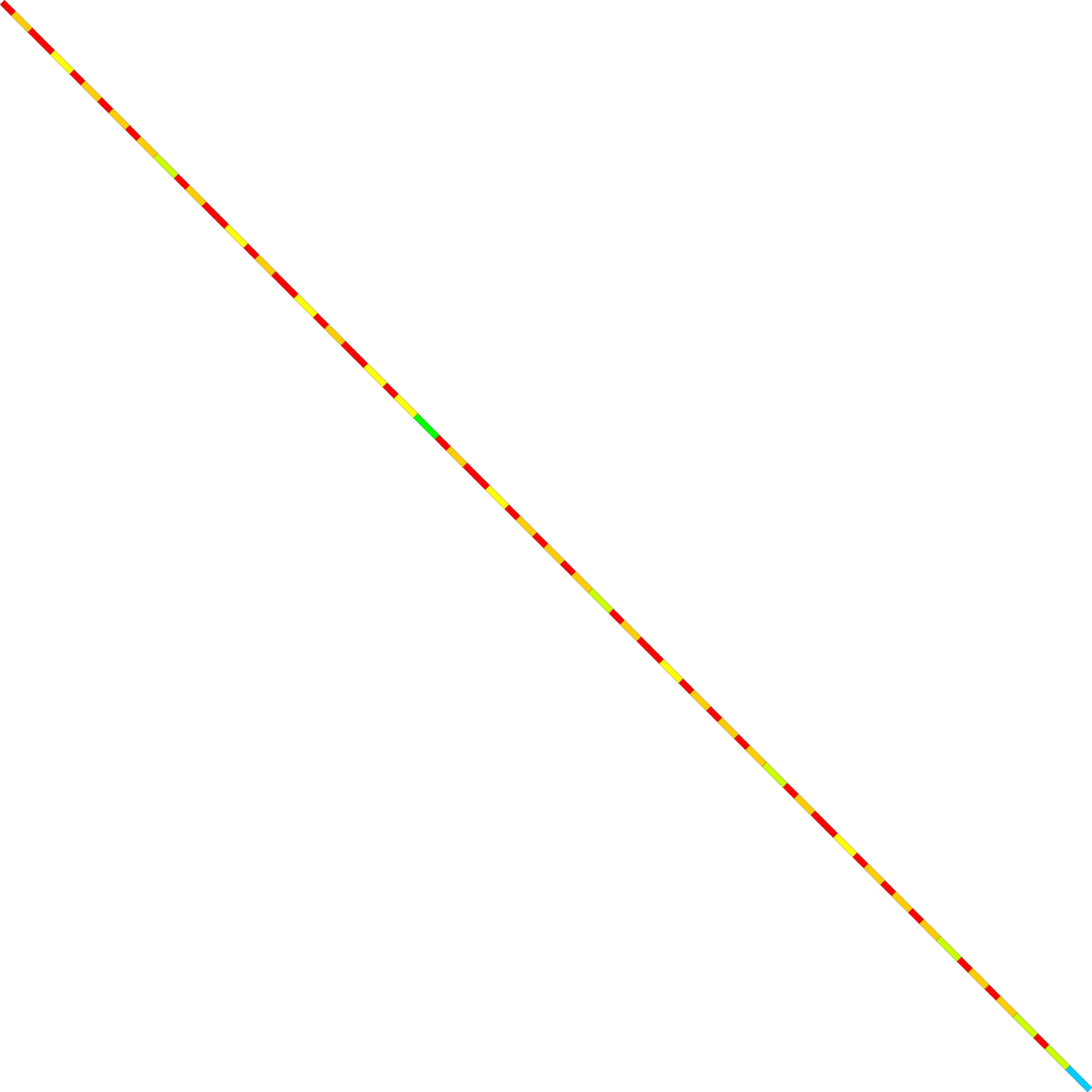
Patch

download vectorformat Infinite Number of Prototiles

---

References

[MRW2021]
Manibo, N. and Rust, D. and Walton J. J.},
Spectral properties of substitutions on compact alphabets
arXiv 2021, https://arxiv.org/abs/2204.07516

[MRW2023]
Manibo, N. and Rust, D. and Walton J. J.},
Spectral properties of substitutions on compact alphabets
Bulletin of the London Mathematical Society 2023, 55(5), pp. 2425-2445, https://doi.org/10.1112/blms.12872

---