Millars n-fold

• Finite Local Complexity
• Finite Rotations
• Polytopal Tiles

Info

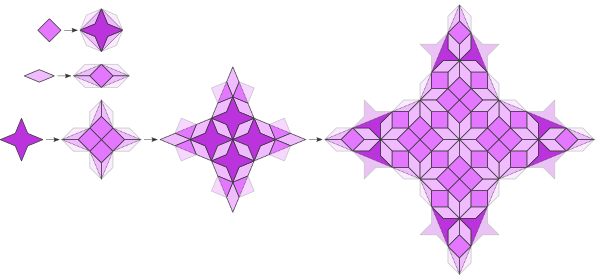
J. Millar discovered a set of tilings with patches of dihedral symmetry $D_2n$ and inflation multiplier $\sqrt{2 + 2 \cos(\frac{\pi}{n})}$, which is the same inflation multiplier as of the Generalized Godreche-Lancon-Billard Binary.

All interior angles of all prototiles are integer multiples of $\frac{\pi}{n}$.

All prototiles have sides with unit length.

All tilings have a prototile in the shape of a rhomb with interior angle $\frac{\pi}{n}$. The longer diagonal also defines the inflation multiplier.

The symmetry of the substitution rules matches the symmetry of the shape of the prototiles.

As an exception J. Millar credits the case $n=6$ to D. Walton.

The example shown below is the tiling for $n=4$. It was also published in Pau2017, but inadvertently without reference to Jim Millar.

Substitution Rule

Patch

download vectorformat Millars n-fold

---

References

[Pau2017]
Pautze, S
Cyclotomic aperiodic substitution tilings
Symmetry 2017, 9(2), doi.org/10.3390/sym9020019

[Mil2020]
Millar, Jim
2n-fold reflectively-symmetric tilings with unit length sides and inflation factor less than 2
2020, https://www.patternblockhead.com/slow%20grow%20tilings.htm

[Mil1998]
Millar, Jim
Octagonal-based set of pieces
1998, https://www.patternblockhead.com/oct.htm

---