Schaad's 7-fold
Discovered by
Info
Schaad’s 7-fold is a variation of Madison’s 7-Fold,
hence it shares many properties with it.
It allows for tilings with global 7-fold symmetry and a lot of locally 7-fold symmetric patches.
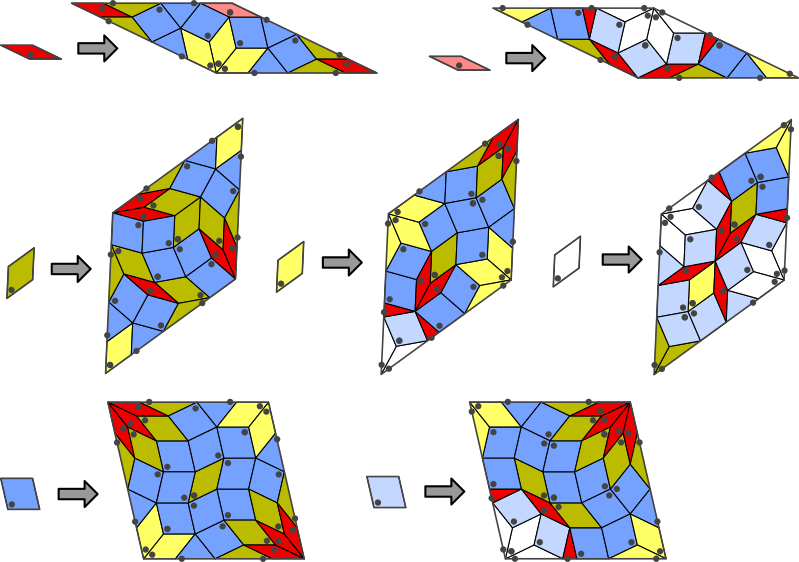
There are three tile shapes, but only seven instead of nine different
prototiles. The inflation factor is a
PV number:
$2+2\cos\left(\frac{\pi}{7}\right)+2\cos\left(\frac{2\pi}{7}\right) = 5.04891733952231\ldots$
which is the largest root of $x^{3}-6x^{2}+5x-1$.
Substitution Rule
Patch
download vectorformat Schaad's 7-fold
References
[ss2022]
P. Stampfli and T. P. Schaad
Ptolemy, the Regular Heptagon, and Quasiperiodic Tilings
Proceedings of Bridges 2022: Mathematics, Art, Music, Architecture, Culture
2022,
39,
135-142,
bridges2022-135.pdf