Watanabe Ito Soma 8-fold
- Finite Local Complexity (FLC)
- Finite Rotations
- Model Set
- Polytopal Tiles
- Rhomb Tiles
- Self-Similar Substitution
Discovered by
Info
This tiling was originally introduced in [WSI87]
, however the description given there admits several substitution rules. This is the version given explicitly in [WSI95]
.
This is an example of a cut and project with a mixed internal space, a product of Euclidean and $p$-adic spaces, namely $\mathbb{R}^2 \times \mathbb{Q}_2$.
Substitution Rule
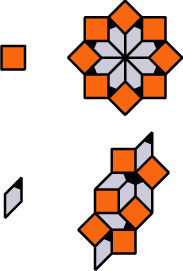
Patch

References
[WSI95]
Watanabe, Y and Soma, T and Ito, M
A new quasiperiodic tiling with dodecagonal symmetry
Acta Crystallogr.
1995,
A51,
pp. 936--942,
[WSI87]
Watanabe, Y and Soma, T and Ito, M
Nonperiodic tessellation with eightfold rotational symmetry
Acta Crystallogr.
1987,
A43,
pp. 133--134,
[WISB1986]
Watanabe, Y. and Ito, M. and Soma, T. and Betsumiya T.
Nonperiodic Tesselation with Eight-fold Rational Symmetry
In Science on Form: Proceedings of the First International Symposium for Science on Form; Ishizaka, S., Kato, Y., Takaki, R., Toriwaki, J., Eds.; KTK Scientific Publishers: Tokyo, Japan
1986,
pp. 471-477,