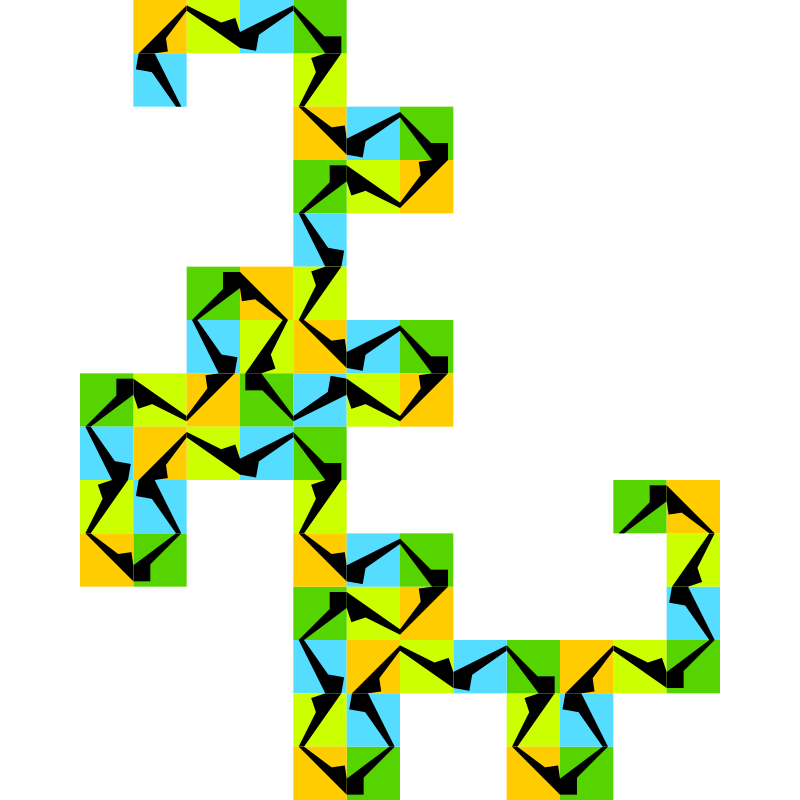Finite Local Complexity (FLC)
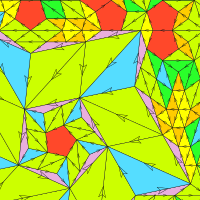
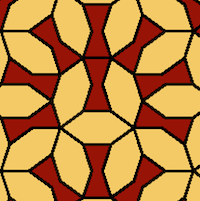
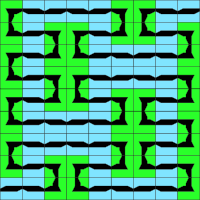
A tiling has finite local complexity (flc) if it contains only finitely many types of patches with diameter less than some given R>0. ‘Types of patches’ is to be read either as congruence classes of patches, or as translation classes of patches. For instance, the pinwheel tiling is not flc w.r.t. translation classes, but it is flc w.r.t. congruence classes. In our classification, this qualifies the pinwheel tiling to be stored under infinite rotations, and there under finite local complexity. Equivalently, one may define flc by requiring that the tiling contains only finitely many n-coronae for a fixed n, or finitely many vertex stars. Here again, one has to consider the distinction between ‘up to congruence’ and ‘up to translation’.